The theoretical resolution of a telescope is determined by the diameter of its aperture, which usually corresponds to the mirror or lens diameter. If the so-called Dawes criterion is used to determine the resolution, it is for green light 117 arcseconds divided by the aperture diameter in mm. For telescopes with 100, 200, and 400 mm aperture, this corresponds to values of 1.1, 0.6 and 0.3 arcseconds. Considering that a seeing of better than 1 arcsecond is the exception rather than the rule due to atmospheric turbulence, it is obvious that already a telescope with an aperture of 100 mm should offer the maximum possible detail recognition in planetary observation. The step to 200 mm aperture should reveal an improvement only under the best conditions. A further increase of the aperture to 400 mm diameter would not bring any further improvement - the resolution would be completely determined by the seeing.

In practice, however, we notice something different: an increase in the aperture (given the same quality of the telescopes) from 100 to 200 mm increases the perception of details enormously, and a further increase to 400 mm brings another considerable improvement, and not only under the very best seeing conditions. What is the reason for this?

To understand this, we need to look more closely at the underlying detail of contrast and contrast transfer through the telescope. A very good introduction to this topic can be found in the highly recommended book "Telescope  Optics" by Harrie Rutten and Martin van  Venrooij  (Willmann-Bell Inc., Richmond, VA, USA). The following reasoning essentially follows that of Martin van  Venrooij  in chapter 18.7 of this book. The contrast between, for example, two surface details of a planet is caused by their different brightness or intensity. The contrast K between a lighter and a darker detail is defined by K=(I_h-I_d)/(I_h+I_d), where I_h and I_d are the respective intensity values. This contrast value ranges from 0 (no conrast) to 1 (maximum contrast). This contrast is transmitted by the telescope into the image plane and the relationship between original contrast and transmitted contrast is described by the so-called contrast transfer function, CTF, (or optical transfer function, OTF, or modulation transfer function, MTF), which results from the underlying physics of wave optics.

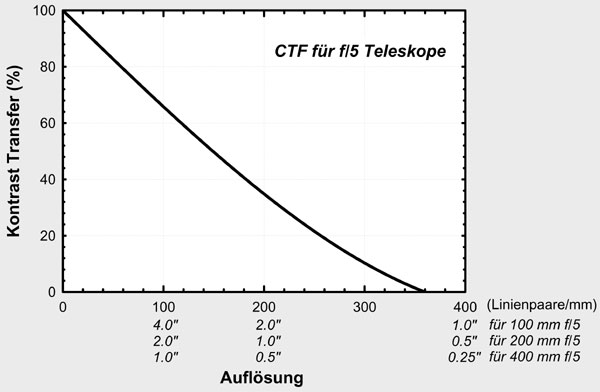
Figure 1: Contrast transfer function for f/5 telescopes depending on the linear resolution and angular resolution for perfect telescopes of 100, 200, and 400 mm aperture.

The CTF provides information on how much of the contrast of a line pattern with an ideal sinusoidal intensity distribution arrives in the image plane, depending on the distance of the lines in this pattern (relative to the image plane) or their apparent angular distance. Such artificial line patterns may seem somewhat bizarre in daily life, but it results directly from the underlying theory. Each image can be divided into a superposition of an infinite number of such line patterns. The technical term for this is Fourier decomposition, which plays a very important role in physics.

Figure 1 shows such a CTF calculated for a perfect telescope with an aperture ration of f/5, depending on the spatial frequency of the line patterns (in pairs of lines per mm), which is independent of the aperture or its angular distance. In terms of angular resolution, the CTF depends on the aperture of the telescope, which is reflected in the different X-axis scales for our standard 100, 200, and 400 mm telescopes. So what does this CTF tell us? First of all, the CTF of our perfect telescopes has a value of 100% only if the number of line pairs per mm goes to zero, corresponding to very large details. For finer details, the contrast transfer decreases continuously and reaches zero at about 360 line pairs per mm. This value also corresponds to the theoretical resolution limit of 1.1, 0.6 and 0.3 arcseconds for our three standard telescopes mentioned above. For comparison only, the diameter of the Airy disc corresponds to a local frequency of about 150 line pairs per mm for our telescopes. 

This tells us that the contrast of finer details is less likely to be transmitted than that of coarser details. The picture thus becomes duller, the finer the details we look at. If we assume a maximum object contrast of 1, then Figure 2 shows what is left of this initial contrast in the image plane.

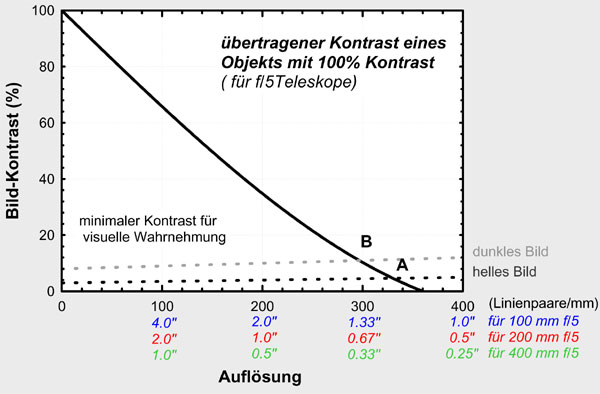
Figure 2

In order for our eye to be able to distinguish two surface details, their image contrast must have a certain minimum value. In his book, Martin van Venrooij  assumes a 5% contrast for fine details and a slightly lower value for coarser details. These values may, of course, vary from observer to observer as well as with external conditions. Details with an image contrast lower than this threshold would therefore no longer be perceived to have different brightness. These minimum values apply to a bright image and correspond to the dashed black line in Figure 2. For a less bright image, the minimum contrast for visual perception is even slightly higher, as indicated by the gray dotted line in Figure 2. At first sight, this is not too bad: the maximum achievable resolution that can be obtained (which is reached as soon as the contrast curve intersects the dashed lines,  i.e. in points A and B, depending on the image brightness) is not far from the theoretical resolution of the optics (intersection of the contrast curve with the X axis). Furthermore, at least with apertures of 200 and 400 mm, it is still better than the limits typically imposed by the seeing.

However, keep in mind: The contrast shown in Figure 2 is the image contrast  transmitted by an object with a maximum contrast of 1. Details, as e.g. banding or whirls in the atmosphere of Jupiter or any other planet, have, however, no intrinsical contrast of 1, but a contrast that is *considerably* lower. Let us look, for example, at the fine details of the whirls in the equatorial bands of Jupiter and assume an intrinsical contrast of 0.1 or 10% for them (which is realistic). The image contrast of an object with an intrinsical contrast of 0.1 can be seen in Figure 3 as a gray solid curve, compared to our previous example with object contrast 1.0 in black.

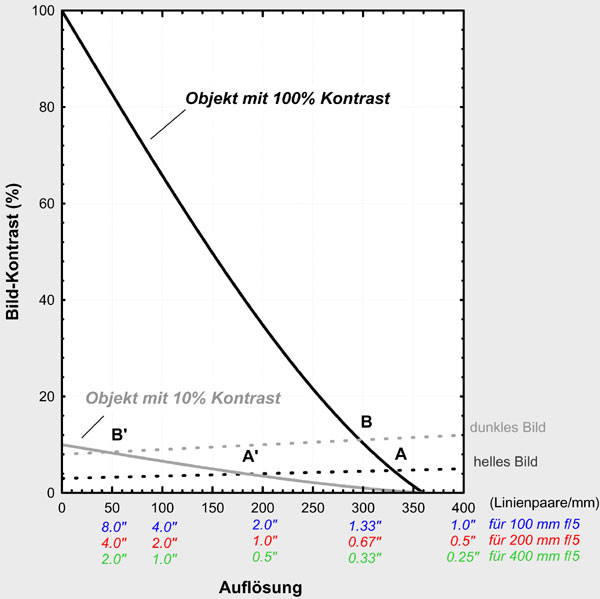
Figure 3

Let us now look again at the maximum resolution that we can obtain and compare it to the Dawes limit. While the intersection A of the black dotted line (for a bright image) with the black contrast curve for the 100% object was still close to the theoretical value, it is now considerably shifted to the left to A'. The visual resolution for a bright image of planetary details with 10% intrinsical contrast is less than 2.0, 1.0 and 0.5 arcseconds for our three standard telescopes. If we continue to take into account that the image (at the same magnification) appears darker in the telescopes with a smaller aperture than, for example, in the 400 mm telescope, the contrast threshold in the smaller telescope will also be higher than in the larger one. The maximum resolution, that can be achieved, thus moves from A' to B' for smaller telescopes. And all of a sudden, it is in a range which it is far from the theoretical Dawes resolution limit of the optics. Even under only moderate seeing conditions, resolution will no longer be determined by the seeing itself, but by the optical properties (primarily the aperture) of the telescope.

The achievable resolution for e.g. planetary details can thus be considerably lower than the theoretical resolution limit of the telescope. It is essentially determined by two factors, namely the image contrast of the details (which in turn depends on the intrinsic contrast of the observed structures) and the contrast threshold of the eye, which depends on the brightness of the image.